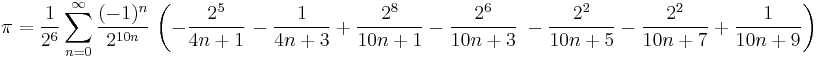Bellard's formula

Bellard's formula, as used by PiHex, the now-completed distributed computing project, is used to calculate the nth digit of π in base 2. It is a faster version (about 43% faster[1]) of the Bailey–Borwein–Plouffe formula. Bellard's formula was discovered by Fabrice Bellard in 1997.

Formula

\begin{align} \pi = \frac1{2^6} \sum_{n=0}^\infty \frac{(-1)^n}{2^{10n}} \, \left(-\frac{2^5}{4n%2B1} \right. & {} - \frac1{4n%2B3} %2B \frac{2^8}{10n%2B1} - \frac{2^6}{10n%2B3} \left. {} - \frac{2^2}{10n%2B5} - \frac{2^2}{10n%2B7} %2B \frac1{10n%2B9} \right) \end{align}

Notes

  1. ^ PiHex Credits

External links